The Normal Distribution.

Density, distribution, quantile, random number generation and parameter estimation functions for the normal distribution. Parameter estimation can be based on a weighted or unweighted i.i.d. sample and can be carried out analytically or numerically.

dNormal(x, mean = 0, sd = 1, params = list(mean, sd), ...)

pNormal(q, mean = 0, sd = 1, params = list(mean, sd), ...)

qNormal(p, mean = 0, sd = 1, params = list(mean, sd), ...)

rNormal(n, mean = 0, sd = 1, params = list(mean, sd), ...)

eNormal(
  X,
  w,
  method = c("unbiased.MLE", "analytical.MLE", "numerical.MLE"),
  ...
)

lNormal(X, w, mean = 0, sd = 1, params = list(mean, sd), logL = TRUE, ...)

sNormal(X, w, mean = 0, sd = 1, params = list(mean, sd), ...)

iNormal(X, w, mean = 0, sd = 1, params = list(mean, sd), ...)

Arguments

x, q: Vector of quantiles.
mean: Location parameter.
sd: Scale parameter.
params: A list that includes all named parameters.
...: Additional parameters.
p: Vector of probabilities.
n: Number of observations.
X: Sample observations.
w: Optional vector of sample weights.
method: Parameter estimation method.
logL: logical; if TRUE, lNormal gives the log-likelihood, otherwise the likelihood is given.

Value

dNormal gives the density, pNormal gives the distribution function, qNormal gives the quantiles, rNormal generates random deviates, and eNormal estimates the parameters. lNormal provides the log-likelihood function, sNormal the score function, and iNormal the observed information matrix.

Details

If the mean or sd are not specified they assume the default values of 0 and 1, respectively.

The dNormal(), pNormal(), qNormal(),and rNormal() functions serve as wrappers of the standard dnorm, pnorm, qnorm, and rnorm functions in the stats package. They allow for the parameters to be declared not only as individual numerical values, but also as a list so parameter estimation can be carried out.

The normal distribution has probability density function $$f(x) = \frac{1}{\sqrt{2 \pi} \sigma} e^{-\frac{(x-\mu)^2}{2\sigma^2}}$$ where $\mu$ is the mean of the distribution and $\sigma$ is the standard deviation. The analytical unbiased parameter estimations are as given by Johnson et.al (Vol 1, pp.123-128).

The log-likelihood function of the normal distribution is given by $$l(\mu, \sigma| x) = \sum_{i}[-0.5 ln(2\pi) - ln(\sigma) - 0.5\sigma^{-2}(x_i-\mu)^2].$$ The score function and observed information matrix are as given by Casella & Berger (2nd Ed, pp.321-322).

References

Johnson, N. L., Kotz, S. and Balakrishnan, N. (1994) Continuous Univariate Distributions, volume 1, chapter 13, Wiley, New York.

Casella, G. and Berger R. L. (2002) Statistical Inference, 2nd Ed, pp.321-322, Duxbury.

Bury, K. (1999) Statistical Distributions in Engineering, Chapter 10, p.143, Cambridge University Press.

Author

Haizhen Wu and A. Jonathan R. Godfrey.
Updates and bug fixes by Sarah Pirikahu.

Examples

# Parameter estimation for a distribution with known shape parameters
x <- rNormal(n=500, params=list(mean=1, sd=2))
est.par <- eNormal(X=x, method="unbiased.MLE"); est.par
#> 
#> Parameters for the Normal distribution. 
#> (found using the  unbiased.MLE method.)
#> 
#>  Parameter     Type  Estimate       S.E.
#>       mean location 0.8937221 0.09463477
#>         sd    scale 2.1160977 0.06698390
#> 
#> 
plot(est.par)


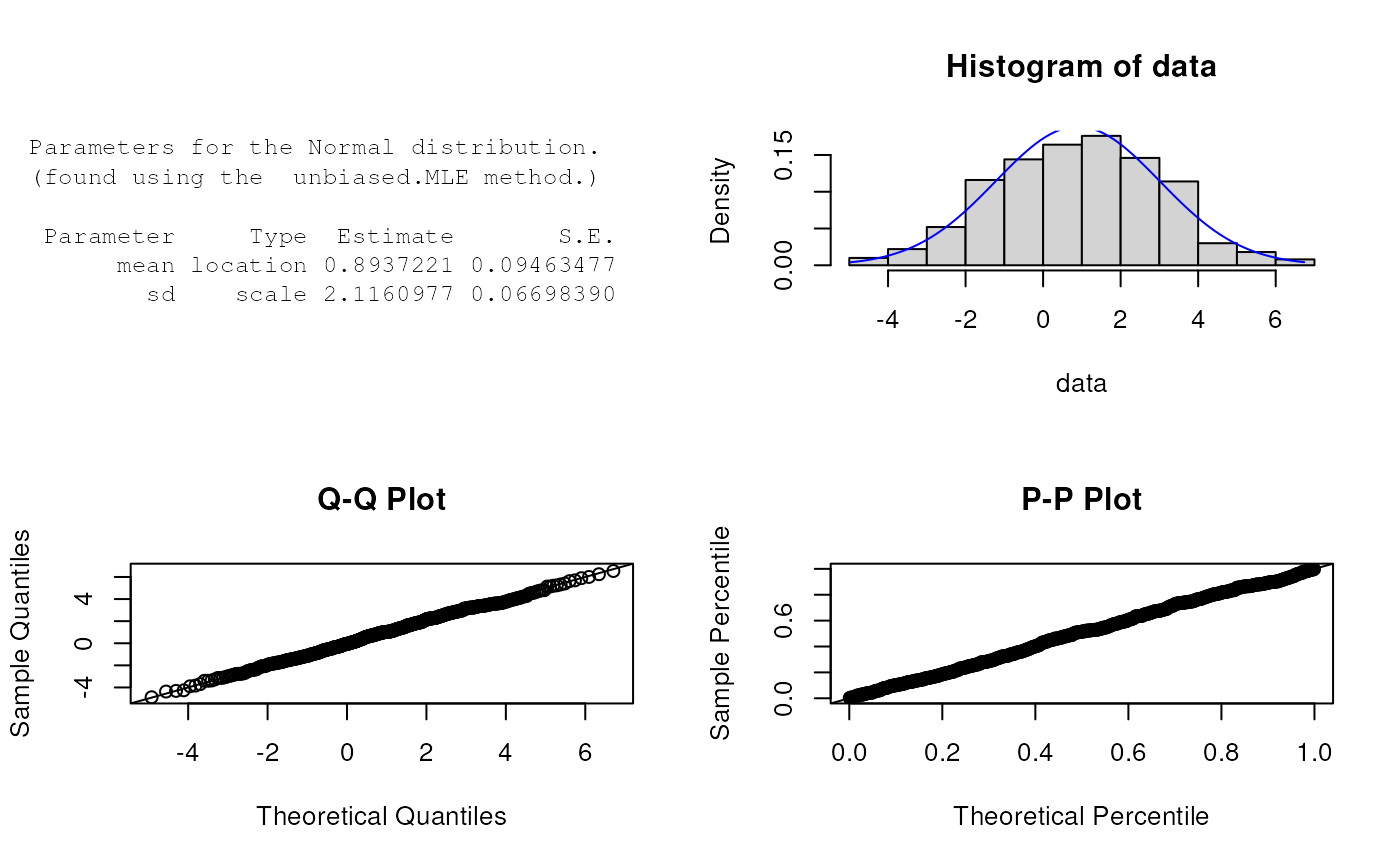#  Fitted density curve and histogram
den.x <- seq(min(x),max(x),length=100)
den.y <- dNormal(den.x, mean = est.par$mean, sd = est.par$sd)
hist(x, breaks=10, probability=TRUE, ylim = c(0,1.2*max(den.y)))
lines(lines(den.x, den.y, col="blue")) # Original data
lines(density(x), col="red")           # Fitted curve


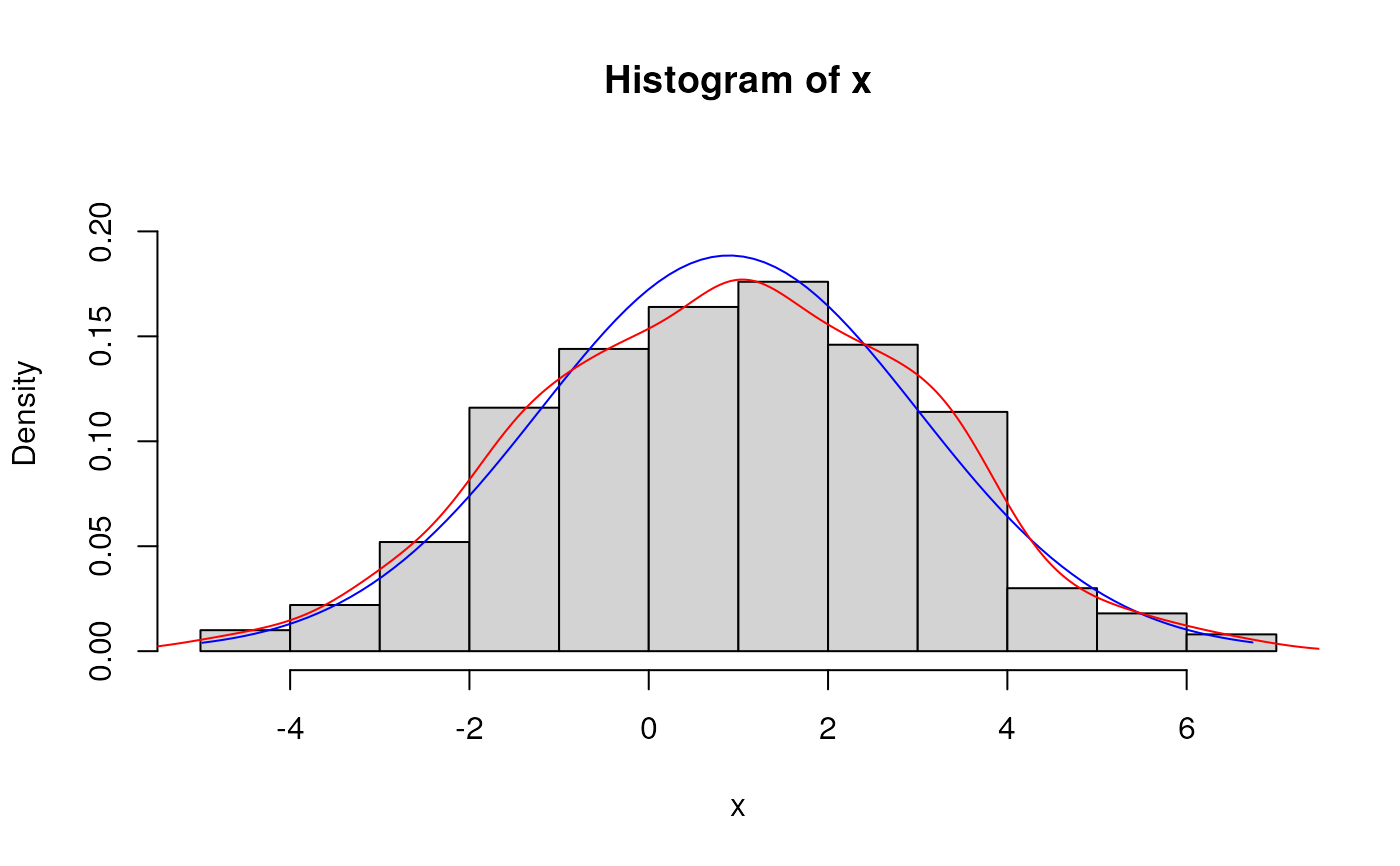# Extracting location and scale parameters
est.par[attributes(est.par)$par.type=="location"]
#> $mean
#> [1] 0.8937221
#> 
est.par[attributes(est.par)$par.type=="scale"]
#> $sd
#> [1] 2.116098
#> 

# Parameter Estimation for a distribution with unknown shape parameters
# Example from: Bury(1999) p.143, parameter estimates as given by Bury are
# mu = 11.984 and sigma = 0.067
data <- c(12.065, 11.992, 11.992, 11.921, 11.954, 11.945, 12.029, 11.948, 11.885, 11.997,
         11.982, 12.109, 11.966, 12.081, 11.846, 12.007, 12.011)
est.par <- eNormal(X=data, method="numerical.MLE"); est.par
#> 
#> Parameters for the Normal distribution. 
#> (found using the  numerical.MLE method.)
#> 
#>  Parameter     Type   Estimate       S.E.
#>       mean location 11.9841176 0.01578771
#>         sd    scale  0.0650944 0.01116360
#> 
#> 
plot(est.par)


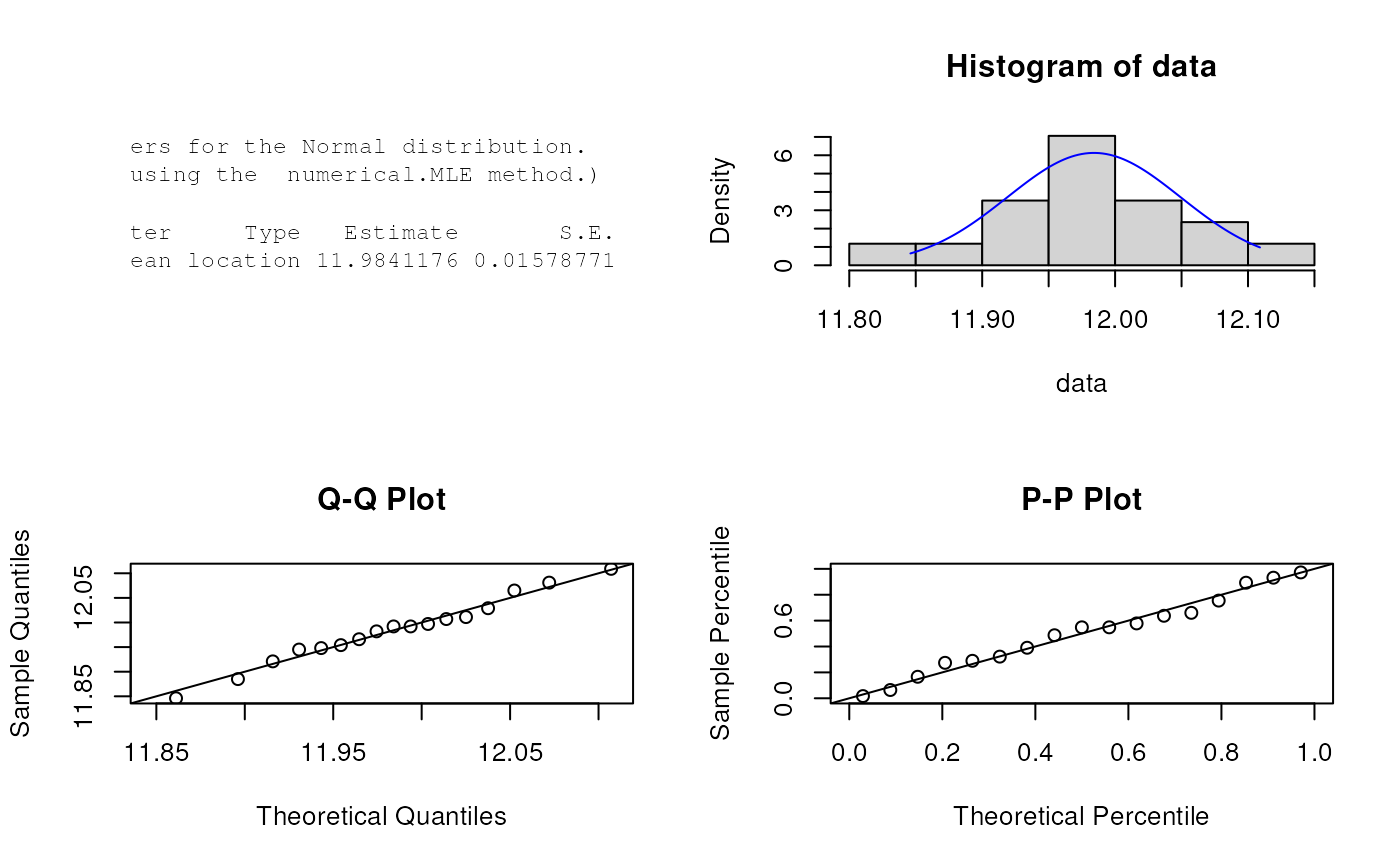# log-likelihood, score function and observed information matrix
lNormal(data, param = est.par)
#> [1] 22.32063
sNormal(data, param = est.par)
#>          mean            sd 
#>  4.051759e-06 -1.505957e-05 
iNormal(data, param = est.par)
#>              mean           sd
#> mean 4.012007e+03 1.244887e-04
#> sd   1.244887e-04 8.024014e+03

# Evaluating the precision of the parameter estimates by the Hessian matrix
H <- attributes(est.par)$nll.hessian; H
#>              mean           sd
#> mean 4.012007e+03 1.244887e-04
#> sd   1.244887e-04 8.024014e+03
var <- solve(H)
se <- sqrt(diag(var)); se
#>       mean         sd 
#> 0.01578771 0.01116360