The Gamma Distribution.

Density, distribution, quantile, random number generation, and parameter estimation functions for the gamma distribution with parameters shape and scale. Parameter estimation can be based on a weighted or unweighted i.i.d sample and can be carried out numerically.

dGamma(x, shape = 2, scale = 2, params = list(shape = 2, scale = 2), ...)

pGamma(q, shape = 2, scale = 2, params = list(shape = 2, scale = 2), ...)

qGamma(p, shape = 2, scale = 2, params = list(shape = 2, scale = 2), ...)

rGamma(n, shape = 2, scale = 2, params = list(shape = 2, scale = 2), ...)

eGamma(X, w, method = c("moments", "numerical.MLE"), ...)

lGamma(
  X,
  w,
  shape = 2,
  scale = 2,
  params = list(shape = 2, scale = 2),
  logL = TRUE,
  ...
)

Arguments

x, q: A vector of quantiles.
shape: Shape parameter.
scale: Scale parameter.
params: A list that includes all named parameters
...: Additional parameters.
p: A vector of probabilities.
n: Number of observations.
X: Sample observations.
w: An optional vector of sample weights.
method: Parameter estimation method.
logL: logical; if TRUE, lBeta_ab gives the log-likelihood, otherwise the likelihood is given.

Value

dGamma gives the density, pGamma the distribution function, qGamma the quantile function, rGamma generates random deviates, and eGamma estimates the distribution parameters.lgamma provides the log-likelihood function.

Details

The dGamma(), pGamma(), qGamma(),and rGamma() functions serve as wrappers of the standard dgamma, pgamma, qgamma, and rgamma functions in the stats package. They allow for the parameters to be declared not only as individual numerical values, but also as a list so parameter estimation can be carried out.

The gamma distribution with parameter shape=$\alpha$ and scale=$\beta$ has probability density function, $$f(x)= (1/\beta^\alpha \Gamma(\alpha))x^{\alpha-1}e^{-x/\beta}$$ where $\alpha > 0$ and $\beta > 0$. Parameter estimation can be performed using the method of moments as given by Johnson et.al (pp.356-357).

The log-likelihood function of the gamma distribution is given by, $$l(\alpha, \beta |x) = (\alpha -1) \sum_i ln(x_i) - \sum_i(x_i/\beta) -n\alpha ln(\beta) + n ln \Gamma(\alpha)$$ where $\Gamma$ is the gamma function. The score function is provided by Rice (2007), p.270.

References

Johnson, N. L., Kotz, S. and Balakrishnan, N. (1995) Continuous Univariate Distributions, volume 1, chapter 17, Wiley, New York.

Bury, K. (1999) Statistical Distributions in Engineering, Chapter 13, pp.225-226, Cambridge University Press.

Rice, J.A. (2007) Mathematical Statistics and Data Analysis, 3rd Ed, Brookes/Cole.

Author

Haizhen Wu and A. Jonathan R. Godfrey.
Updates and bug fixes by Sarah Pirikahu, Oleksii Nikolaienko.

Examples

# Parameter estimation for a distribution with known shape parameters
X <- rGamma(n=500, shape=1.5, scale=0.5)
est.par <- eGamma(X, method="numerical.MLE"); est.par
#> 
#> Parameters for the Gamma distribution. 
#> (found using the  numerical.MLE method.)
#> 
#>  Parameter  Type  Estimate       S.E.
#>      shape shape 1.5092211 0.08693682
#>      scale scale 0.5011912 0.03415262
#> 
#> 
plot(est.par)


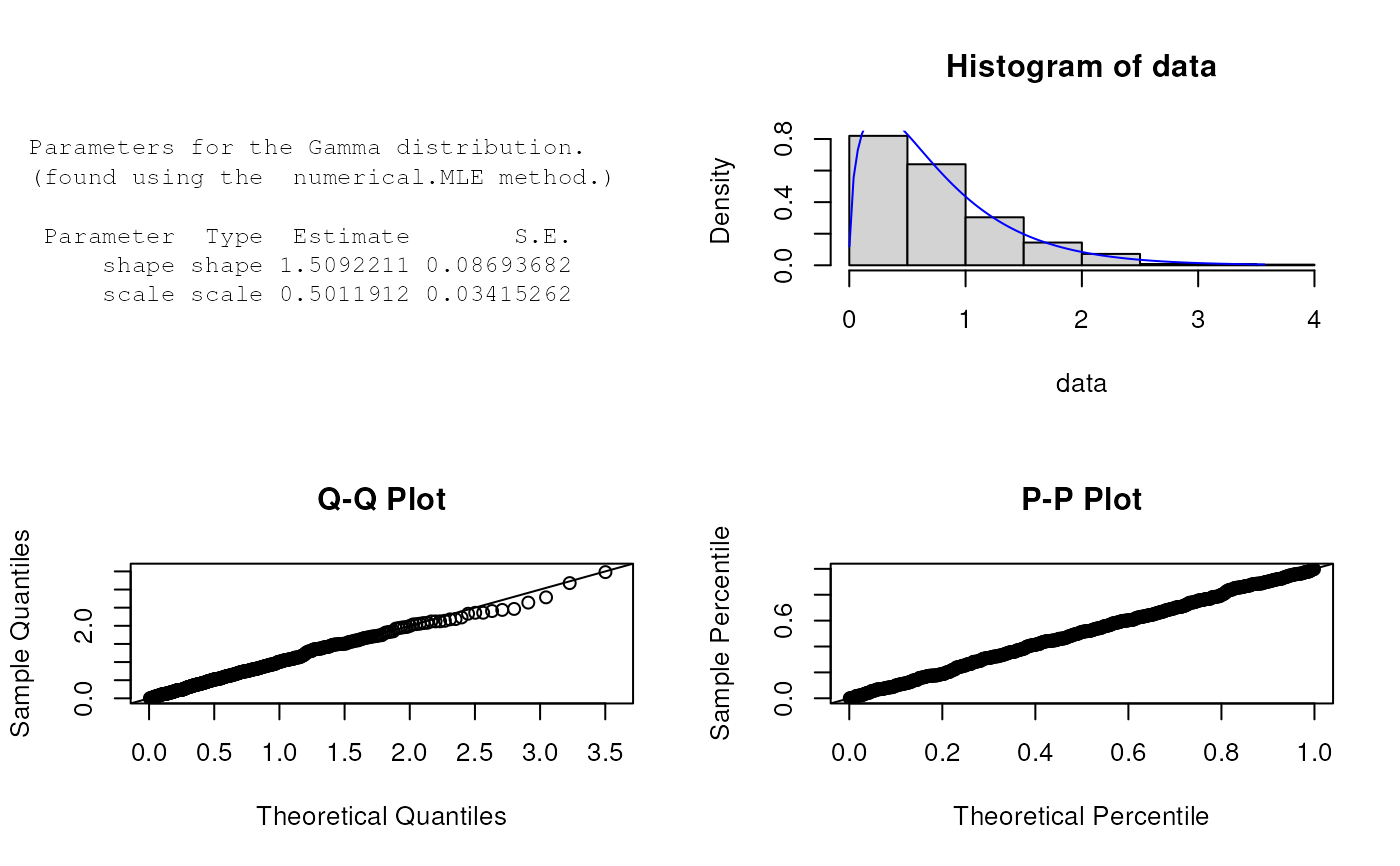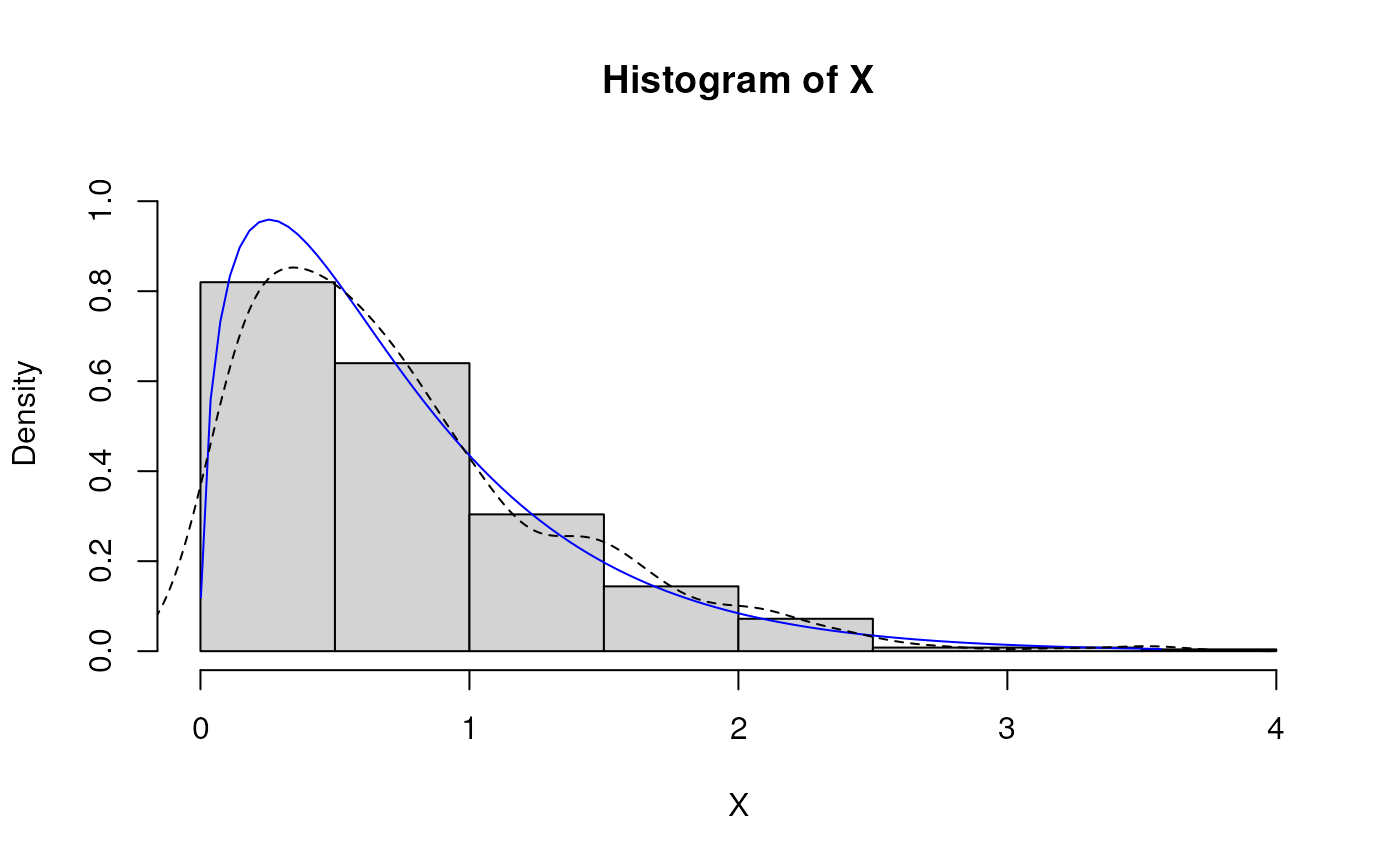
#  Fitted density curve and histogram
den.x <- seq(min(X),max(X),length=100)
den.y <- dGamma(den.x,shape=est.par$shape,scale=est.par$scale)
hist(X, breaks=10, probability=TRUE, ylim = c(0,1.1*max(den.y)))
lines(den.x, den.y, col="blue")
lines(density(X), lty=2)


# Extracting shape or scale parameters
est.par[attributes(est.par)$par.type=="shape"]
#> $shape
#> [1] 1.509221
#> 
est.par[attributes(est.par)$par.type=="scale"]
#> $scale
#> [1] 0.5011912
#> 

# Parameter estimation for a distribution with unknown shape parameters
# Example from:  Bury(1999) pp.225-226, parameter estimates as given by Bury are
# shape = 6.40 and scale=2.54.
data <- c(16, 11.6, 19.9, 18.6, 18, 13.1, 29.1, 10.3, 12.2, 15.6, 12.7, 13.1,
         19.2, 19.5, 23, 6.7, 7.1, 14.3, 20.6, 25.6, 8.2, 34.4, 16.1, 10.2, 12.3)
est.par <- eGamma(data, method="numerical.MLE"); est.par
#> 
#> Parameters for the Gamma distribution. 
#> (found using the  numerical.MLE method.)
#> 
#>  Parameter  Type Estimate      S.E.
#>      shape shape 6.404003 1.7661637
#>      scale scale 2.544659 0.7300405
#> 
#> 
plot(est.par)


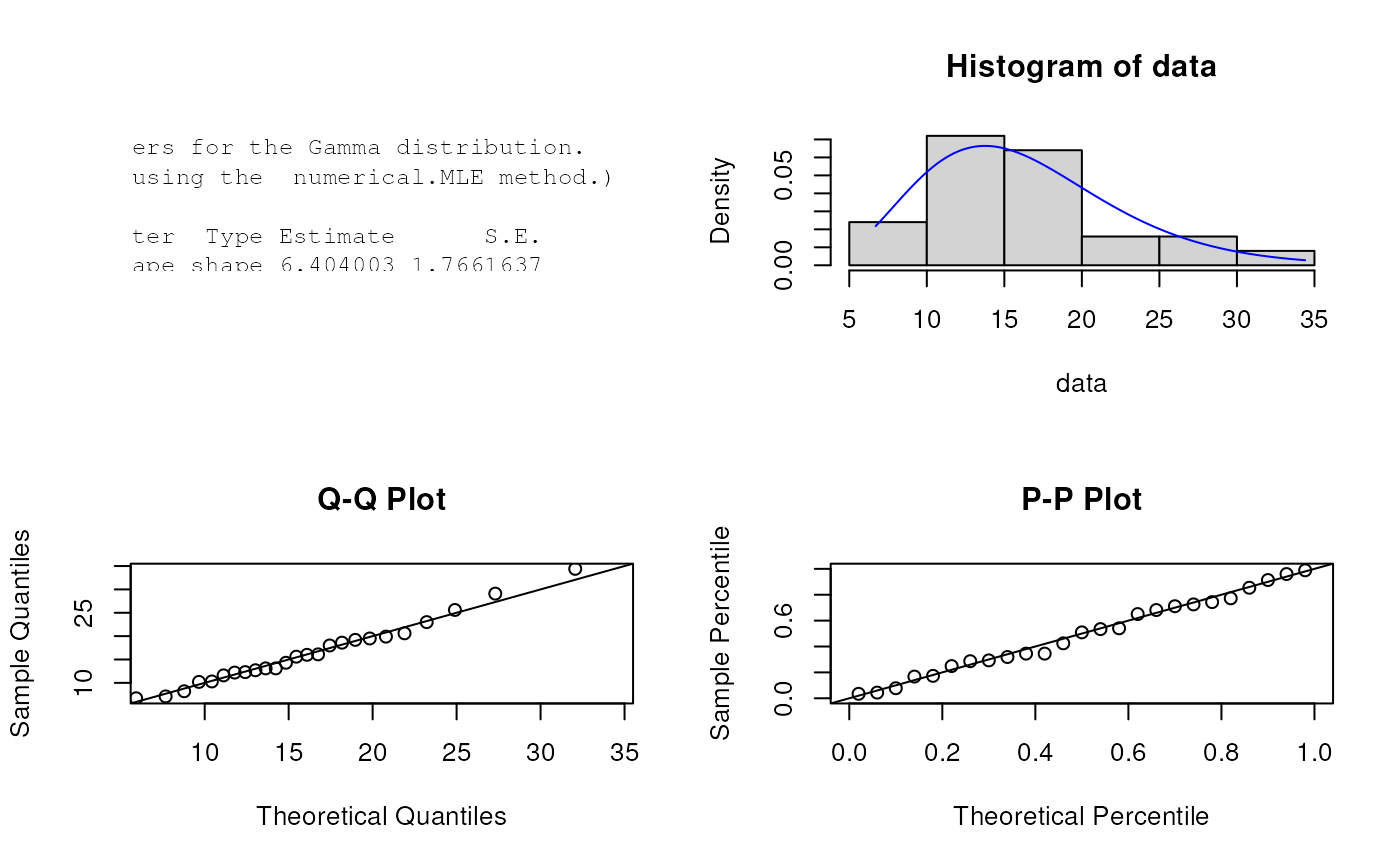# log-likelihood
lGamma(data,param = est.par)
#> [1] -80.68186

# Evaluating the precision of the parameter estimates by the Hessian matrix
H <- attributes(est.par)$nll.hessian
var <- solve(H)
se <- sqrt(diag(var));se
#>     shape     scale 
#> 1.7661637 0.7300405